Pages : 1 - 2 - 3

Enigme 21G : Les faucheurs
Une équipe de faucheurs avait à faucher deux prés dont l'un était deux fois plus grand que l'autre. Durant une moitié de la journée, l'équipe a fauché une partie du grand pré. Ensuite elle s'est divisée en deux groupes égaux. Les faucheurs de la première équipe sont restés sur le grand pré qu'ils ont fini de faucher vers le soir ; ceux du second ont fauché le deuxième pré également jusqu'au soir, mais il en est resté une parcelle qu'un faucheur a terminée le lendemain en une journée de travail. Combien de faucheurs y avait-il dans l'équipe ?

Enigme 22G : Un cube et un carré avec si peu d'allumettes ?
Faire un cube avec 5 allumettes et un carré avec 3 allumettes sans les casser bien entendu !

Enigme 23G : Les billes
Dans mon panier, il y a des billes bleues, des rouges, des jaunes et des noires, une seule bille verte et moins de six oranges. Il y a trois fois plus de billes bleues que de billes rouges et deux fois plus de billes jaunes que d'oranges. Au total, il y a quarante-deux billes. À présent, j'y ajoute deux billes de couleur orange, six de couleur bleue, quatre jaunes, cinq vertes et trois rouges. Il y a alors dans mon panier autant de billes jaunes que de billes rouges. Je remarque que si l'on écrit de la gauche vers la droite, les uns à la suite des autres, le nombre de billes jaunes, puis celui de billes noires, puis celui de bleues, et enfin de vertes, on obtient un nombre qui est un carré parfait. Combien y a-t-il de billes noires dans mon panier ?

Enigme 24G : L'automobile
Une automobile se trouve à 1 km d'une ville. A 1 km de la ville (la où est la voiture) se trouve 1 panneau de signalisation : 120km/h. A 1/2km: 1 panneau de 60km/h ; à 1/3km : 40km/h; à 1/4km: 30km/h; à 1/5km: 24km/h et à 1/6km: 20km/h. En supposant qu'elle roule à la vitesse maximale, combien de temps mettra-t-elle pour arriver à la ville ?

Enigme 25G : Les tas de feuilles
Deux hommes ratissent leurs jardins l'un fait 3 tas de feuilles et l'autre 7 lorsqu'ils mettront leurs tas en commun, combien de tas y aura-t-il ?

Enigme 26G : Les 31 maillons de la chaîne
Je possède un collier qui se présente sous la forme d'une chaîne fermée de 31 maillons. Pour rémunérer une personne qui travaillera pour moi pendant 31 jours, je dois lui donner chaque soir un maillon de cette chaîne. Quel est le nombre minimum de maillons à couper pour tenir mes engagements et à quel endroit dois-je les couper ? (La personne peut rendre des maillons, par exemple un soir elle peut vous rendre 2 maillons et vous lui donner une chaînette de 3 maillons).

Enigme 27G : Des trains, encore et toujours !
Nous sommes dans une ligne de métro circulaire. 24 trains s'y déplacent dans la même direction à intervalles réguliers et roulant tous à la même vitesse. Demain, on doit rajouter des trains afin de diminuer de 20% les intervalles entre deux trains. Combien y aura-t-il de trains supplémentaires demain?

Enigme 28G : Le rectangle
On plie soigneusement en deux une feuille de papier rectangulaire, cinq fois à la suite, en pliant à chaque fois suivant un pli perpendiculaire au pli précédent. Après cela on déchire les 4 coins du (petit) rectangle de papier obtenu. Ceci fait on déplie la feuille. Combien de vrais trous voit-on alors à l'intérieur de la feuille de papier?

Enigme 29G : Les tonneaux de vin
Trois hommes ont à partager 21 tonneaux dont il y en a 7 pleins, 7 vides et 7 pleins à demi. Comment se peut faire le partage en sorte que tous les 3 aient un égal nombre de tonneaux et égale quantité de vin?

Enigme 30G : L'arbre foudroyé
Un arbre de 8 mètres de hauteur a été brisé par le vent. Le sommet touche la terre à 4 mètre du pied de l'arbre. A quelle hauteur a-t-il été brisé ?

Enigme 31G : Les deux mâts
Un mât de 3 mètres et un mât de 6 mètres sont plantés verticalement sur un terrain plat. Deux cordes relient les sommets de chaque mât au bas de l'autre. A quelle hauteur se trouve le point d'intersection des deux cordes?

Enigme 32G : L'allumette et les 2 verres
Placer une allumette entre 2 verres retournés, l'allumette ne doit pas toucher le sol ou la table. Comment faire tenir l'allumette en enlevant un verre, avec l'aide seule d'une autre allumette ?

Enigme 33G : Encore des allumettes
Comment faire 5 triangles équilatéraux avec 9 allumettes ?

Enigme 34G : Le code secret
Sur le point de mourir, un vieil avare s'avise que son fils, qui est en voyage, ne sache pas où il a dissimulé le magot. Il n'ose confier, ni de vive voix ni par écrit, le secret de sa cachette à l'un de ses voisins pourtant dévoués. Il décide pourtant de donner à l'un d'eux la lettre suivante à charge de la remettre à son fils à son retour :
"Mon cher fils. Avant de mourir, je veux te dire où se trouve ce que je te laisse. Grâce aux indications que tu trouveras ci-après, et que je te fais parvenir par le biais de notre voisin de droite, tu n'auras pas de grandes difficultés à entrer en possession de ton héritage. Ton Père affectionné."
L  H  E  T  A  T  O  T
E  A  E  T  U  F  E  U
H  M  T  E  E  N O  M
S  E  E  R  S  C  E  R
E  C  D  M O  O  A  A
L  R  A  E  A   I   U  C
A  A  D  L  L   R  S  S
E  V  C  E  I   E   C  I
A son retour, le fils se gratte la tête, lit et relit la lettre et soudain, il a une illumination. Le secret de la lettre était simple en effet. A votre tour, pouvez-vous découvrir où est le trésor ?

Enigme 35G : La fausse pièce, le retour...
On vous donne 12 pièces de monnaie dont une est fausse mais on ne sait pas si elle est plus légère ou plus lourde que les autres. Vous êtes muni d'une balance à deux plateaux, comment pouvez-vous trouver la fausse pièce en seulement trois pesées ?

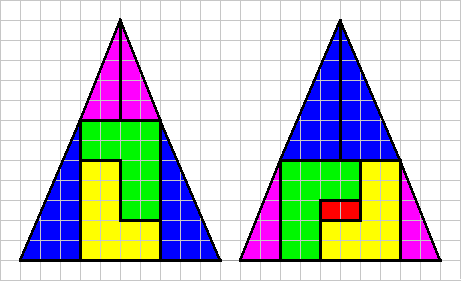
Enigme 36G : Le triangle de Curry
La première figure est composée de 6 morceaux représentant au total 60 cm², la deuxième qui est pourtant faite avec les mêmes morceaux mais disposés autrement, voit sa surface augmentée de 2 cm² (le petit rectangle rouge). Comment est-ce possible ?

Enigme 37G : Le carré et l'anneau
On a un carré de verre de 24 cm de côté et un anneau de 5 cm de diamètre intérieur. Comment découper le carré en quatre morceaux égaux de façon à ce qu'ils puissent tous passer dans l'anneau sans se briser.

Enigme 38G : Huit reines sur un échiquier
Comment disposer huit reines sur un échiquier de façon à ce qu'aucune d'entre elles ne soit mise en échec par une autre ? Je vous rappelle que les reines se déplacent en ligne droite et en diagonale.

Enigme 39G : Les carrés
Combien y a-t-il de carrés, au total, dans la figure précédente ?

Enigme 40G : Le ver et l'encyclopédie en 10 volumes
Une encyclopédie en dix volumes est rangée dans l'ordre sur une planche de bibliothèque. Chaque volume est épais de 4,5 cm pour les feuilles et de deux fois 0,25 cm pour la couverture. Un vers né en page 1 du volume 1 se nourrit en traversant perpendiculairement et en ligne droite la collection complète et meurt à la dernière page du dixième volume. Quelle distance aura-t-il parcourue pendant son existence ?